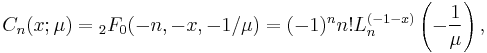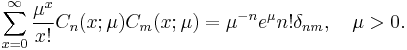Charlier polynomials

In mathematics, Charlier polynomials (also called Poisson–Charlier polynomials) are a family of orthogonal polynomials introduced by Carl Charlier. They are given in terms of the generalized hypergeometric function by

$C_n(x; \mu)= {}_2F_0(-n,-x,-1/\mu)=(-1)^n n! L_n^{(-1-x)}\left(-\frac 1 \mu \right),\,$

where $L$ are Laguerre polynomials. They satisfy the orthogonality relation

$\sum_{x=0}^\infty \frac{\mu^x}{x!} C_n(x; \mu)C_m(x; \mu)=\mu^{-n} e^\mu n! \delta_{nm}, \quad \mu>0.$

References

C. V. L. Charlier (1905–1906) Uber die Darstellung willkurlicher Funktionen, Ark. Mat. Astr. och Fysic 2 , 20.
Koornwinder, Tom H.; Wong, Roderick S. C.; Koekoek, Roelof; Swarttouw, René F. (2010), "Hahn Class: Definitions", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F. et al., NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0521192255, MR 2723248, http://dlmf.nist.gov/18.19
Szego, Gabor (1939), Orthogonal Polynomials, Colloquium Publications - American Mathematical Society, ISBN 978-0-8218-1023-1, MR 0372517